The Effects of the Learning Rate on Model Performance

6 min readSep 3, 2020

สำหรับผู้อ่านบางท่านที่เริ่มต้นศึกษา Machine Learning Model อาจจะเคยสับสนกับคำว่า Parameter และ Hyperparameter ว่า 2 ตัวนี้มีความแตกต่างกันอย่างไร

Parameter => เป็นตัวแปร (Variable) ที่อยู่ภายใน Model เช่น Weight และ Bias ซึ่งจะถูกประมาณค่าโดยอัตโนมัติจาก Dataset ที่ใช้สอนโดยตรง
Hyperparameter => เป็นตัวแปรภายนอก Model เช่น Learning Rate, Droupout Rate, จำนวน Hidden Layer, ชนิดของ Loss Function ฯลฯ ซึ่งไม่ได้เกิดจากการประมาณค่าโดยตรงจาก Dataset

Learning Rate

เป็น Hyperparameter ที่สำคัญตัวหนึ่ง ที่มีหน้าที่ในการปรับขนาดของ Error ในแต่ครั้งของการปรับปรุง Weight และ Bias ด้วย Back-propagation Algorithm ดังสมการต่อไปนี้

Update w = w - Learning_Rate*Error_at_w

ซึ่งการปรับเปลี่ยน Learning Rate จะมีผลกระทบกับประสิทธิภาพของ Model เป็นอย่างมาก ถ้าให้เลือกว่าจะปรับจูน Hyperparameter ตัวไหนก่อน Learning Rate คงเป็น Hyperparameter ตัวแรกๆ ที่ควรจะพิจารณาครับ
ในบทนี้ผู้อ่านจะได้ทำความเข้าใจผลลัพธ์ที่เกิดจากการปรับเปลี่ยนค่า Learning Rate ด้วยวิธีการต่างๆ ได้แก่ Momentum, Learning Rate Decay, การลด Learning Rate เมื่อเจอกับที่ราบสูง (Plateau) และการใช้ Adaptive Learning Rate Algorithm เพื่อปรับค่า Learning Rate แบบอัตโนมัติ

Impact of Learning Rate

เราจะใช้ Learning Rate ควบคุมความเร็วในการปรับตัวของ Model ต่อปัญหาที่มันจะต้องแก้ โดยการกำหนด Learning Rate ขนาดเล็ก จะทำให้ในการ Train แต่ละรอบมันจะปรับปรุง Weight และ Bias ทีละนิด จึงต้องการจำนวน Epoch หลายรอบ ขณะที่การกำหนด Learning Rate ขนาดใหญ่ จะทำให้ในการ ิ แต่ละรอบจะมีการปรับปรุง Weight และ Bias อย่างรวดเร็ว จึงต้องการจำนวน Epoch ที่น้อยกว่า
ใน Keras Framework ผู้อ่านสามารถกำหนดค่าเริ่มต้นของ Learning Rate ได้ผ่าน Stochastic Gradient Descent Algorithm ต่างๆ อย่างเช่น SGD, AdaGrad (Adaptive Gradient Algorithm), RMSprop (Root Mean Square Propagation) หรือ Adam (Adaptive Moment Estimation) ฯลฯ โดยเราจะเรียก Algorithm เหล่านี้ว่า Optimizer
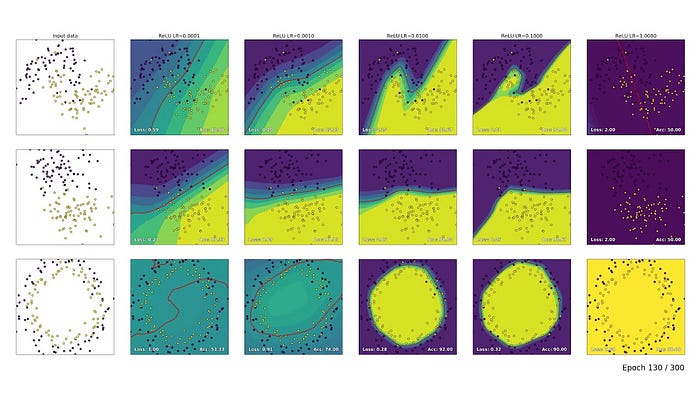
โดยเราจะสร้าง Neural Network อย่างง่ายเพื่อจำแนกข้อมูลที่มี 3 Class ด้วยการทดลองปรับ Learning Rate ตั้งแต่ 1.0 ถึง 0.000001 ผ่าน SGD Optimizer (Optimizer พื้นฐานที่เราสามารถปรับ Learning Rate ได้ด้วยตัวเอง)

เราจะใช้ make_blobs() Function ของ scikit-learn Library ในการสร้าง Dataset ขนาด 2 มิติ ที่มี 3 Class

from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.utils import to_categorical

from sklearn.datasets import make_blobs
from matplotlib import pyplot
from numpy import where

from sklearn.model_selection import train_test_split

import pandas as pd
import plotly.express as pxX, y = make_blobs(n_samples=3000, centers=3, n_features=2, cluster_std=2, random_state=2)

แล้วแยก Dataset เป็น 2 ส่วน สำหรับการ Train 60% และสำหรับการ Test อีก 40%

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, shuffle= True)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

นำ Dataset ส่วนที่ Train มาแปลงเป็น DataFrame โดยเปลี่ยนชนิดข้อมูลใน Column Class เป็น String เพื่อทำให้สามารถแสดงสีแบบไม่ต่อเนื่องได้ แล้วนำไป Plot

X_train_pd = pd.DataFrame(X_train, columns=['x', 'y'])
y_train_pd = pd.DataFrame(y_train, columns=['class'])

df = pd.concat([X_train_pd, y_train_pd], axis=1)
df["class"] = df["class"].astype(str)fig = px.scatter(df, x="x", y="y", color="class")
fig.show()

เราจะเข้ารหัสผลเฉลย แบบ One-Hot Encoder เพื่อที่ว่าเมื่อ Model มีการ Pridict ว่าเป็น Class ไหน มันจะให้ค่าความมั่นใจ (Confidence) กลับมาด้วยทุกครั้ง

y_train = to_categorical(y_train)
y_test = to_categorical(y_test)

นิยาม Model, Complie และ Plot Accuracy

def fit_model(trainX, trainy, testX, testy, lrate):
    model = Sequential()
    model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))
    
    opt = SGD(lr=lrate)
    model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

    history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

    pyplot.plot(history.history['accuracy'], label='train')
    pyplot.plot(history.history['val_accuracy'], label='test')
    pyplot.title('lr='+str(lrate), pad=-35)
 

learning_rates = [1E-0, 1E-1, 1E-2, 1E-3, 1E-4, 1E-5, 1E-6, 1E-7]
for i in range(len(learning_rates)):
    plot_no = 420 + (i+1)
    pyplot.subplot(plot_no)
    fit_model(X_train, y_train, X_test, y_test, learning_rates[i])
pyplot.tight_layout()
pyplot.savefig('lr1.jpeg', dpi=300)
pyplot.show()

เมื่อ Train เสร็จแล้ว ผู้อ่านจะเห็นค่า Accuracy หรือ Learning Curve ของ Model ดังภาพ

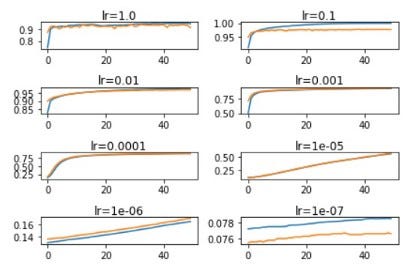
จากภาพด้านบน จะเห็นว่าที่ lr = 1.0 หน้าตา Learning Curve ของ Model มีการแกว่งขึ้นลงอย่างน่าตกใจ และที่ lr = 1E-6 และ 1E-7 นั้น Model มีอัตราการเรียนรู้ค่อนข้างต่ำ โดยที่ lr = 0.1, 0.01 และ 0.001 เห็นได้ว่า Model จะประสบความสำเร็จในการเรียนรู้ที่แตกต่างกันไป โดยที่ lr = 0.1, Model จะมีอัตราการเรียนรู้เร็วที่สุด

Momentum

Momentum (β) เป็นเทคนิคในการลดการแกว่งของ Learning Curves พร้อมกับเร่งอัตราการเรียนรู้ของ Model ให้เร็วขึ้น โดยใช้ Velocity (ความเร็ว) ของรอบก่อนหน้า และ Velocity ในรอบปัจจุบันเพื่อปรับปรุง Weight และ Bias ในน้ำหนักที่ไม่เท่ากัน ซึ่งโดยปกติจะมีการให้น้ำหนัก Velocity ในรอบก่อนหน้ามากกว่า เช่น ถ้ากำหนด β = 0.9 แสดงว่าเราจะให้น้ำหนัก Velocity ในรอบก่อนหน้าเท่ากับ 0.9 และ Velocity ในรอบปัจจุบันเท่ากับ 0.1 ดังสมการต่อไปนี้

where

นิยาม Model, กำหนด lr = 0.01, Complie และ Plot Accuracy

def fit_model(trainX, trainy, testX, testy, momentum):
    model = Sequential()
    model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))

    opt = SGD(lr=0.01, momentum=momentum)
    model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

    history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

    pyplot.plot(history.history['accuracy'], label='train')
    pyplot.plot(history.history['val_accuracy'], label='test')
    pyplot.title('momentum='+str(momentum), pad=-80)
 
momentums = [0.0, 0.5, 0.9, 0.99]
for i in range(len(momentums)):
    plot_no = 220 + (i+1)
    pyplot.subplot(plot_no)

    fit_model(X_train, y_train, X_test, y_test, momentums[i])

pyplot.tight_layout()
pyplot.savefig('momentum.jpeg', dpi=300)
pyplot.show()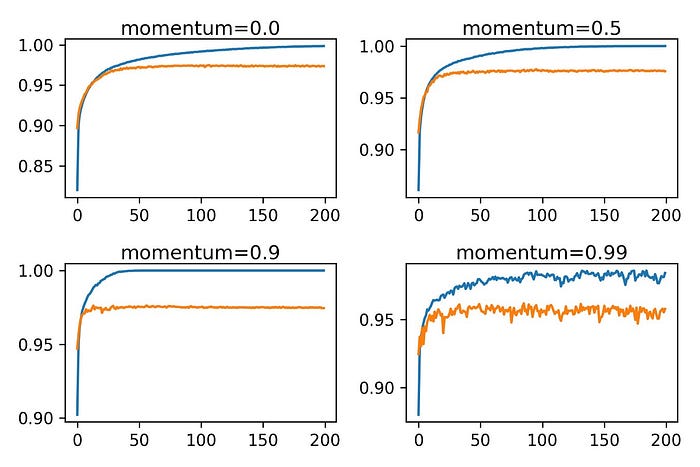

จากภาพด้านบน จะเห็นว่าที่ momentum (β) = 0.9 หน้าตา Learning Curves ของ Model มีการแกว่งที่น้อยลง พร้อมกับมีอัตราการเรียนรู้ที่เร็วขึ้น เมื่อเทียบกับตอนที่ไม่ได้ใช้ momentum อย่างเห็นได้ชัด

Learning Rate Decay

นอกจากนี้เรายังสามารถเพิ่มประสิทธิภาพของ Model ได้โดยการค่อย ๆ ลด Learning Rate (Learning Rate Decay) ในแต่ละ Epoch ในอัตราที่เหมาะสม เช่นดังแสดงในตัวอย่างต่อไปนี้

def decay_lrate(initial_lrate, decay, iteration):
    return initial_lrate * (1.0 / (1.0 + decay * iteration))
 
decays = [1E-1, 1E-2, 1E-3, 1E-4]
lrate = 0.01
n_updates = 200
for decay in decays:
    
    lrates = [decay_lrate(lrate, decay, i) for i in range(n_updates)]
    
    pyplot.plot(lrates, label=str(decay))
pyplot.legend()
pyplot.savefig('decay.jpeg', dpi=300)
pyplot.show()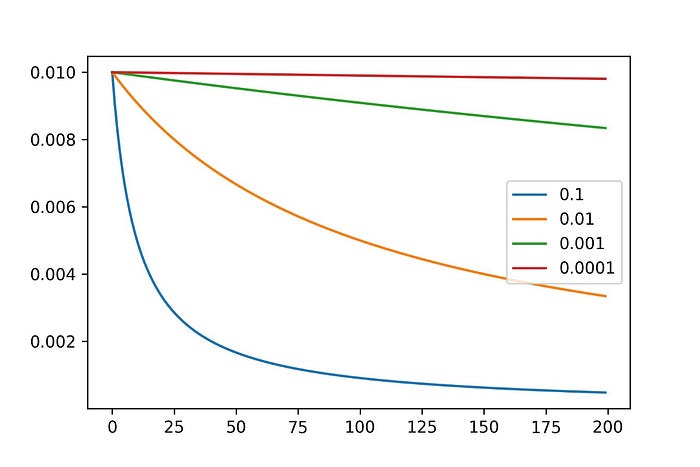

นิยาม Model, กำหนด lr = 0.01, Complie และ Plot Accuracy

def fit_model(trainX, trainy, testX, testy, decay):
    model = Sequential()
    model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))

    opt = SGD(lr=0.01, decay=decay)
    model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
    
    history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

    pyplot.plot(history.history['accuracy'], label='train')
    pyplot.plot(history.history['val_accuracy'], label='test')
    pyplot.title('decay='+str(decay), pad=-80)
 

decay_rates = [1E-1, 1E-2, 1E-3, 1E-4]
for i in range(len(decay_rates)):
    plot_no = 220 + (i+1)
    pyplot.subplot(plot_no)
    fit_model(X_train, y_train, X_test, y_test, decay_rates[i])

pyplot.legend()
pyplot.savefig('decay2.jpeg', dpi=300)
pyplot.show()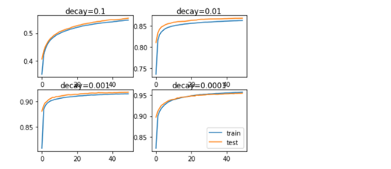

จากภาพด้านบน จะเห็นว่าที่ decay = 0.001 และ 0.0001 นั้น Learning Curves ของ Model ในรอบหลังๆ มีการแกว่งที่น้อยลง พร้อมกับมีค่า Accuracy ที่สูงขึ้นกว่าเมื่อเทียบกับตอนที่ไม่ได้ใช้ decay ครับ

Drop Learning Rate on Plateau

ในกรณีที่พบว่า Loss Value ไม่มีการลดลงในระยะเวลาหนึ่ง หรือเราเรียกสถานการนี้ว่าเมื่อเจอกับที่ราบสูง (Plateau) เช่น เมื่อ Train Model ผ่านไปแล้ว 5 Epoch (patience=5) เราจะใช้เทคนิคการปรับลดค่า Learning Rate โดยใช้ค่า factor เป็นตัวปรับลดน้ำหนักของ Learning Rate เช่น กำหนดให้ factor = 0.1 เดิม Learning Rate มีค่าเท่ากับ 0.01 เมื่อผ่านไป 5 Epoch Learning Rate จะถูกปรับลดเป็น 0.001 (0.01*0.1) เพื่อทำให้ Loss Value สามารถลดลงได้อีกครั้ง ตามตัวอย่างต่อไปนี้

from tensorflow.keras.callbacks import Callback
from tensorflow.keras.callbacks import ReduceLROnPlateau
from tensorflow.keras import backendclass LearningRateMonitor(Callback):
    def on_train_begin(self, logs={}):
        self.lrates = list()
 
    def on_epoch_end(self, epoch, logs={}):
        optimizer = self.model.optimizer
        lrate = float(backend.get_value(self.model.optimizer.lr))
        self.lrates.append(lrate)
 
def fit_model(trainX, trainy, testX, testy, patience):
    model = Sequential()
    model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))

    opt = SGD(lr=0.01)
    model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy'])

    rlrp = ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=patience, min_delta=1E-7)
    lrm = LearningRateMonitor()
    history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0, callbacks=[rlrp, lrm])
    return lrm.lrates, history.history['loss'], history.history['accuracy']
 

def line_plots(patiences, series, st):
    for i in range(len(patiences)):
        pyplot.subplot(220 + (i+1))
        pyplot.plot(series[i])
        pyplot.title('patience='+str(patiences[i]), pad=-80)
    pyplot.legend()
    pyplot.savefig('patience.jpeg', dpi=300)
    pyplot.show()
 
patiences = [2, 5, 10, 15]
lr_list, loss_list, acc_list, = list(), list(), list()
for i in range(len(patiences)):
    lr, loss, acc = fit_model(X_train, y_train, X_test, y_test, patiences[i])
    lr_list.append(lr)
    loss_list.append(loss)
    acc_list.append(acc)

line_plots(patiences, lr_list, 'lr')

line_plots(patiences, loss_list, 'loss')

line_plots(patiences, acc_list, 'acc')

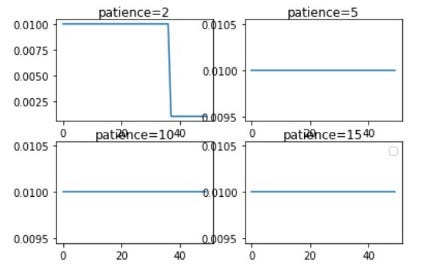
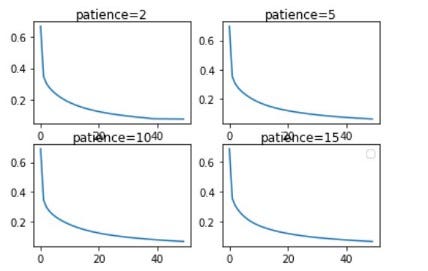
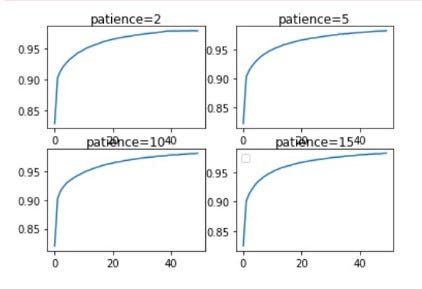
จากภาพด้านบน จะเห็นว่า เมื่อกำหนด patience เท่ากับ 10 แล้ว Loss Value จะลดลงถึง 0.4 ซึ่งจะทำให้ Accuracy มีค่าเพิ่มขึ้นไปด้วย

Adaptive Learning Rates Gradient Descent

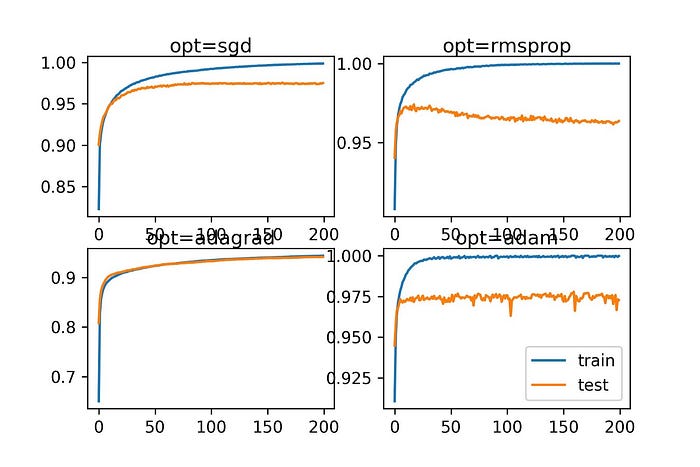
ในการทดลองสุดท้ายของบทความนี้เราจะใช้ Stochastic Gradient Descent Algorithm ต่างๆ ได้แก่ AdaGrad (Adaptive Gradient Algorithm), RMSprop (Root Mean Square Propagation) และ Adam (Adaptive Moment Estimation) Optimizer ซึ่งเป็น Adaptive Learning Rate Algorithm สำหรับปรับค่า Learning Rate เปรียบเทียบกับการปรับค่าเองโดยใช้ SGD

def fit_model(trainX, trainy, testX, testy, optimizer):
    model = Sequential()
    model.add(Dense(50, input_dim=2, activation='relu', kernel_initializer='he_uniform'))
    model.add(Dense(3, activation='softmax'))

    model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
    
    history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=200, verbose=0)

    pyplot.plot(history.history['accuracy'], label='train')
    pyplot.plot(history.history['val_accuracy'], label='test')
    pyplot.title('opt='+optimizer, pad=-80)

momentums = ['sgd', 'rmsprop', 'adagrad', 'adam']
for i in range(len(momentums)):
    plot_no = 220 + (i+1)
    pyplot.subplot(plot_no)

    fit_model(X_train, y_train, X_test, y_test, momentums[i])

pyplot.legend()
pyplot.savefig('adaptive.jpeg', dpi=300)    
pyplot.show()

The Effects of the Learning Rate on Model Performance

Learning Rate

Impact of Learning Rate

เราจะใช้ make_blobs() Function ของ scikit-learn Library ในการสร้าง Dataset ขนาด 2 มิติ ที่มี 3 Class

Momentum

Learning Rate Decay

Drop Learning Rate on Plateau

Adaptive Learning Rates Gradient Descent

สำหรับวันนีี้ก็มีเพียงเท่านี้ครับ

>> ขอบคุณที่เรียนรู้ <<

Written by Phakorn